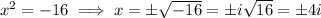Divide both sides by -3, and replace
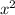 with
with
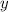 . Then
. Then
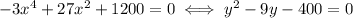
Factorize the quadratic in
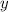 to get
to get
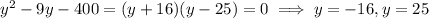
which in turn means
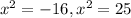
But
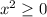 for all real
for all real
 , so we can ignore the first solution. This leaves us with
, so we can ignore the first solution. This leaves us with
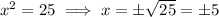
If we allow for any complex solution, then we can continue with the solution we ignored: