Question

Three geometric sequences are given below.

Sequence A: 160,40,10,2.5,...
Sequence B: -21,63,-189,567,...
Sequence C: 8,12,18,27,....

Order the sequences from least common ratio to the greatest common ratio.

Answer 1

A C B

Explanation:

In sequence A. the numbers are being divided by 4.

In sequence B. the numbers are being multiplied by -3

In sequence C. the numbers are being add by 4

So the ratio from least to greatest would be A C B

Answer 2

Sequence B, Sequence A, Sequence C

Explanation:

Common ratio of a geometric sequence is the ratio of a term and its previous term of the sequence.

Thus, the common ratio of the sequence A: 160,40,10,2.5,...

`r_1=(40)/(160)=(1)/(4)`

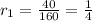
The common ratio of the sequence B: -21,63,-189,567,...

`r_2=(63)/(-21)=-3`

The common ratio of the sequence C : 8,12,18,27,....

`r_3=(12)/(8)=(3)/(2)`

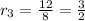
Since, -3 <
`(1)/(4)` <
`(3)/(2)`

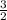
Thus,

`r_2 < r_1 < r_3`

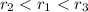
Hence, the order the sequences from least common ratio to the greatest common ratio is,

Sequence B, Sequence A, Sequence C