Question

Find the number of sides of a regular polygon, whose each exterior angle has a
measure of 40°.

Answer 1

Answer :
9
Explanation :

Number of sides = 360/exterior angle

So, n= 360/40=9

So the regular polygon has 9 sides.

Answer 2

`\large \bf \implies{9}`

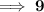
Explanation:

Given :

• angle 40°

To Find :

• number of sides of a regular polygon, whose each exterior angle has a measure of 40°

Solution :

Since, the given polygon is a regular polygon.

It's each exterior angle is equal.

Sum of all the exterior angles = 360°

Number of exterior angles =
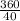`(360\degree)/(40\degree)` = 9°

`\longrightarrow`Number of sides = 9

Hence, it is nonagon.