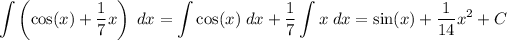Question

Please help with the questions in the image

Answer 1

First integral:

Use the rational exponent to represent roots. You have

`\displaystyle \int\sqrt[8]{x^9}\;dx = \int x^{(9)/(8)}\;dx`

And from here you can use the rule

`\displaystyle \int x^n\;dx=(x^(n+1))/(n+1)+C`

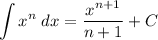
to derive

`\displaystyle \int\sqrt[8]{x^9}\;dx = \frac{x^{(17)/(8)}}{(17)/(8)}=\frac{8x^{(17)/(8)}}{17}`

Second integral:

Simply split the fraction:

`(3+√(x)+x)/(x)=(3)/(x)+(√(x))/(x)+(x)/(x)=(3)/(x)+(1)/(√(x))+1`

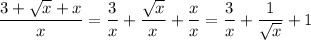
So, the integral of the sum becomes the sum of three immediate integrals:

`\displaystyle \int (3)/(x)\;dx = 3\log(|x|)+C`

`\displaystyle \int (1)/(√(x))\;dx = \int x^{-(1)/(2)}\;dx = 2√(x)+C`

`\displaystyle \int 1\;dx = x+C`

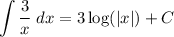
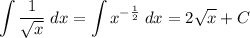
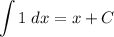
So, the answer is the sum of the three pieces:

`3\log(|x|) + 2√(x) + x+C`

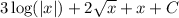
Third integral:

Again, you can split the integral of the sum in the sum of the integrals. The antiderivative of the cosine is the sine, because
`\sin'(x)=\cos(x)`. So, you have

`\displaystyle \int \left( \cos(x)+(1)/(7)x\right)\;dx = \int \cos(x)\;dx + (1)/(7)\int x\;dx = \sin(x)+(1)/(14)x^2+C`