Question

Jana is proving that the following trigonometric identity is true:

cos(−θ)⋅tanθ=sinθ

Which step would be the first line of her proof?

cos(−θ)⋅tanθ=sin(−θ)
cosθ⋅tan(−θ)=sinθ
cosθ⋅tanθ=sinθ
cos(−θ)⋅tan(−θ)=sinθ

Answer 1

Answer c is the right answer .

Answer 2

The first line of her proof is
`\cos\theta \tan\theta =\sin\theta`

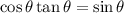
Explanation:

The given trigonometric identity is
`\cos(-\theta) \tan\theta =\sin\theta`.

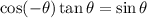Jana has to recall that, the cosine function is an even function.

For that matter,
`\cos(-\theta)=\cos(\theta)`.

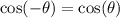Jana has to apply this property by substituting
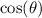`\cos(\theta)` for
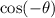`\cos(-\theta)` in the given identity to obtain,

`\cos\theta \tan\theta =\sin\theta`.

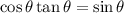Note that, the sine and the tangent functions are odd functions, therefore,

`\sin(-\theta)=-\sin(\theta)`

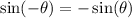
and

`\tan(-\theta)=-\tan(\theta)`

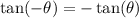
Hence, the correct answer is option C.