Answer: Choice D
4x - 3y = 15
====================================================
Step-by-step explanation:
The two points (-1,-1) and (2,3) are marked on the line
Let's find the slope of the line through those two points.
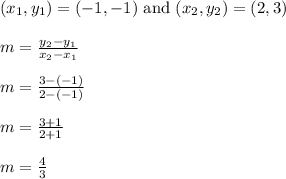
The slope is 4/3 meaning we go up 4 and to the right 3.
-------------
Parallel lines have equal slopes, but different y intercepts. We'll need to see which of the four answer choices have a slope of 4/3.
Solve the equation in choice A for y. The goal is to get it into y = mx+b form so we can determine the slope m.
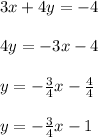
Equation A has a slope of -3/4 and not 4/3 like we want.
Therefore, this answer choice is crossed off the list.
Follow similar steps for choices B through D. I'll show the slopes of each so you can check your work.
- slope of equation B is 3/4
- slope of equation C is -4/3
- slope of equation D is 4/3
We have a match with equation D. Therefore, the equation 4x-3y = 15 is parallel to the given line shown in the graph.
You can use graphing tools like Desmos or GeoGebra to confirm the answer.