Question

The highway forming three cities form a right triangle.Walnut Grove is 91.7 miles from Pecan City and 52.4 miles from Almondville. Pecan City is 75.3 miles from Almondville. A road is being planned to connect Almondville to the highway running between Walnut Grove and Pecan City. What is the shortest length possible for that road? Round your answer to the nearest tenth.

Answer 1

Answer: 43.02 miles (Approx)

Explanation:

Let the entire situation is shown by a triangle CAB,

In which A shows Almondville, B shows Walnut Grove and C shows Pecan City.

Also,
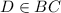`D\in BC` such that
`AD\perp BC`

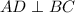
Thus, According to the question, AB = 52.4 miles

AC = 75.3 miles and BC = 91.7 miles.

And, We have to find out AD = ?

Since, CAB and CDA are right angle triangles.

Where, ∠CAB≅∠CDA

∠ACB≅∠ACD

Thus, By AA similarity postulate,

`\triangle CAB\sim \triangle CDA`

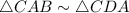
Therefore, by the property of similarity,

`(AB)/(DA) = (CB)/(AC)`

⇒
`(52.4)/(DA) = (91.7)/(75.3)`

⇒
`DA= (75.3* 52.4)/(91.7)`

⇒
`DA= (3945)/(91.7)`

⇒
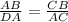
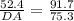
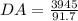
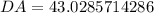`DA= 43.0285714286`≈ 43.02 miles

Thus, the shortest length possible for that road= 43.02 miles (approx)

Answer 2

The shortest length possible for that road is 43.0 miles

Explanation:

Please, see the attached file.

Thanks.