Question

A farmer plants apple, pear, and cherry trees in an orchard. The number of apple trees is 8 more than twice the number of pear trees. The number of cherry and pear trees combined is 11 more than the number of apple trees. The farmer plants 143 trees total. How many of each type of tree did the farmer plant in the orchard?

Answer 1

Let x represents the number of apple tree and y represents the number of pear tree and z represents the number of cherry tree in an orchard.

From the given statement: The number of apple trees is 8 more than twice the number of pear trees.

⇒
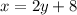`x = 2y + 8` .....[1]

Also, It is given that the number of cherry and pear trees combined is 11 more than the number of apple trees.

⇒
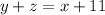`y + z = x + 11` ......[2]

The farmer plants 143 trees total.

⇒
`x +y +z =143` .....[3]

Substitute equation [2] into [3] we get;

`x + x + 11 = 143`

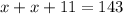
Combine like terms;

`2x +11 = 143`

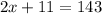
Subtract 11 on both sides we get;

2x + 11 -11 =143 -11

Simplify:

2x = 132

Divide both sides by 2 we get;

x = 66

Substitute the value of x in equation [1];

66 = 2y + 8

Subtract 8 on both sides we get;

`66 -8 =2y + 8 -8`

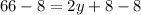
Simplify:

58 = 2y

Divide by 2 on both sides we get;

y = 29

Substitute the value of x and y in equation [3];

we have;

29 + 66 + z = 143

95 + z =143

Subtract 95 on both sides, we get;

95+ z -95 = 143- 95

Simplify:

z = 48

The framer plant in the orchard = 66 apple trees , 29 pear trees and 48 cherry trees