Question

An element with mass 640 grams decays by 7.3% per minute. How much of the element is remaining after 8 minutes, to the nearest 10th of a gram?

Answer 1

349.0 grams to nearest tenth

Explanation:

After each minute there will be (100- 7.3) = 92.7 % ( or 0.927) of the element left.

Therefore after 8 minutes amount left = 640*0.927^8

= 349.0 grams answer

Answer 2

Answer: 349.0 gms.

Explanation:

The exponential decay equation is given by :-

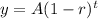`y=A(1-r)^t` , where A= Initial value , r = rate of decay in decimal and t is time.

As per given , we have

A= 640 gm

r= 7.3%=0.073

Then , our decay function will become :-

`y=640(1-0.073)^t\\\\\Rightarrow\ y=640(0.927)^8`

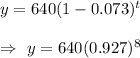
At t= 8 minutes, we have

`y=640(0.927)^8= 348.993908894\approx349.0`

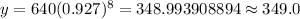
Hence, after 8 minutes , the remaining amount of element = 349.0 gms.