Question

Suppose Company A produces packages of throat lozenges that are normally distributed with a mean of 38.2 individual lozenges and a standard deviation of 1.7 lozenges. Company B produces packages of throat lozenges that are normally distributed with a mean of 36.9 individual lozenges and a standard deviation of 2.2 lozenges.

Which company would be more likely to produce a package of 43 throat lozenges?
Company A is more likely; its z-score of -2.82 is closer to the mean than Company B's z-score of -2.77.

Company B is more likely; its z-score of -2.77 is closer to the mean than Company A's z-score of -2.82.

Company A is more likely; its z-score of 2.82 is closer to the mean than Company B's z-score of 2.77.

Company B is more likely; its z-score of 2.77 is closer to the mean than Company A's z-score of 2.82.

Answer 1

B,A,B

Step-by-step explanation:

>:) Did The Test

Answer 2

The correct option is:

Company B is more likely; its z-score of 2.77 is closer to the mean than Company A's z-score of 2.82.

Step-by-step explanation:

The company's whose z score would be closer to 0 would be more likely to produce the package of 43 throat lozenges

The z score for the company A is:

`z=(43-38.2)/(1.7) =2.82`

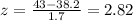
While the z score for the company B is:

`z=(43-36.9)/(2.2)=2.77`

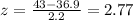
Since the z score of company B is closer to 0 than the company A, therefore the company is more likely