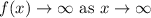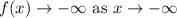Question

Which statement correctly describes the end behavior of f(x)=ax+b, where a and b are positive numbers?

As x→∞, f(x)→∞, and as x→−∞, f(x)→∞.
As x→∞, f(x)→∞, and as x→−∞, f(x)→−∞.
As x→∞, f(x)→−∞, and as x→−∞, f(x)→∞.
As x→∞, f(x)→−∞, and as x→−∞, f(x)→−∞.

Answer 1

The correct option is 2.

Explanation:

The given function is

`f(x)=ax+b`

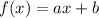
Where, a and b are positive numbers.

The given function is the slope intercept form of a linear function. Where a is the slope and b is y-intercept.

Since slope is positive therefore function approaches to infinity as x approaches to infinity and function approaches to negative infinity as x approaches to negative infinity.

It is also proved by using limits.

`lim_(x\rightarrow \infty)f(x)=lim_(x\rightarrow \infty)(ax+b)`

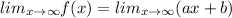
Apply limits.

`lim_(x\rightarrow \infty)f(x)=a(\infty)+b=\infty`

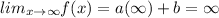
Similarly,

`lim_(x\rightarrow -\infty)f(x)=lim_(x\rightarrow -\infty)(ax+b)`

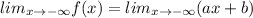
Apply limits.

`lim_(x\rightarrow -\infty)f(x)=a(-\infty)+b=-\infty`

Therefore option 2 is correct.

`f(x)\rightarrow \infty \text{ as }x\rightarrow \infty`

`f(x)\rightarrow -\infty \text{ as }x\rightarrow -\infty`