Question

Parallelogram ABCD has vertices at A(2,-3), B(8, -6), C(14,-3), and D(8,0).

SELECT THE OPTION WHICH BEST COMPLETES THE TWO FOLLOWING STATEMENTS:

The answer options are in the pic ^

Answer 1

#1) are equal; #2) are NOT opposite reciprocals

Explanation:

To find the slopes, we use the formula

`m=(y_2-y_1)/(x_2-x_1)`

For the slope from A to B,

m = (-3--6)/(2-8) = (-3+6)/(-6) = 3/-6 = -0.5

For the slope from B to C,

m = (-6--3)/(8-14) = (-6+3)/(-6) = -3/-6 = 0.5

For the slope from C to D,

m = (-3-0)/(14-8) = -3/6 = =-0.5

For the slope from D to A,

m = (0--3)/(8-2) = (0+3)/6 = 3/6 = 0.5

The slopes are NOT negative reciprocals.

To find the distances, we use the formula

`d=√((y_2-y_1)^2+(x_2-x_1)^2)`

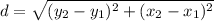
For the distance from A to B,

`d=√((-3--6)^2+(2-8)^2)=√((-3+6)^2+(-6)^2)=√(3^2+(-6)^2)\\\\=√(9+36)=√(45)=3√(5)`

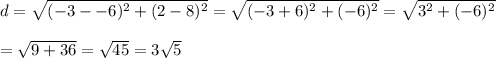
For the distance from B to C,

`d=√((-6--3)^2+(8-14)^2)=√((-6+3)^2+(-6)^2)=√((-3)^2+(-6)^2)\\\\=√(9+36)=√(45)=3√(5)`

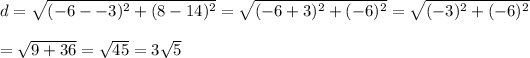
For the distance from C to D,

`d=√((-3-0)^2+(14-8)^2)=√((-3)^2+6^2)=√(9+36)=√(45)\\\\=3√(5)`

For the distance from D to A,

`d=√((0--3)^2+(8-2)^2)=√((0+3)^2+6^2)=√(3^2+6^2)\\\\=√(9+36)=√(45)=3√(5)`

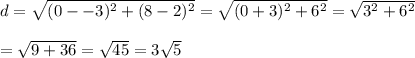
The lengths of two consecutive sides are the same.

Answer 2

Answer: Option C is the correct answer.

Explanation: