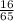Question

Given cos a= 3/5, sin B = 5/13 and a and B are first quadrant angles find cos(a + B)

A. 1/3
B. 16/65
C. -33/65

Please explain

Answer 1

Option B is correct.

Value of cos(a+B) is,
`(16)/(65)`

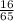
Explanation:

Using the formula:

`\cos(a+B) = \cos a \cos B -\sin a \sin B`

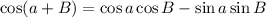
Given the values:

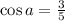`\cos a = (3)/(5)` and
`\sin B = (5)/(13)`

Using trigonometric identity:

`\sin^2 \theta + \cos^2 \theta =1`

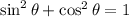
or

`\sin \theta = √(1-\cos^2 \theta)`

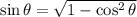
or

`\cos \theta = √(1-\sin^2 \theta)`

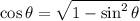
Find the value of sin a and cos B;

Using trigonometric identity:

`\sin a = √(1-\cos^2 a)`

`\sin a = \sqrt{1-((3)/(5))^2}` =
`\sqrt{1-(9)/(25)} = \sqrt{(25-9)/(25)}=\sqrt{(16)/(25) } =(4)/(5)`

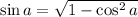
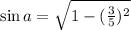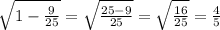
Similarly;

`\cos B = √(1-\sin^2 B)`

`\cos B = \sqrt{1-((5)/(13))^2}` =
`\sqrt{1-(25)/(169)} = \sqrt{(169-25)/(169)}=\sqrt{(144)/(169) } =(12)/(13)`

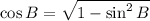
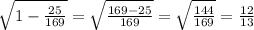
Substitute these given values equation [1] we have;

`\cos(a+B) =(3)/(5) \cdot (12)/(13)-(4)/(5) \cdot (5)/(13)`

`\cos(a+B) =(36)/(65)-(20)/(65)`

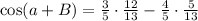
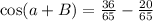
then;

`\cos(a+B) =(36-20)/(65)=(16)/(65)`

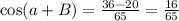
Since, the angles a and B are in first quadrant angles therefore the value of cos(a+B) is,
`(16)/(65)`