Answer:
The 13.2 meters from that point on the ocean floor to the wreck.
Explanation:
As given
A ship's sonar finds that the angle of depression to a ship wrack on the bottom of the ocean is 12.5°.
If a point on the ocean floor is 60 meters.
Now by using the trigonometric identity.

As shown in the figure given below.
Perpendicular = CB
Base = AC = 60 meters
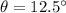
Put in the identity
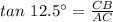
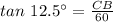
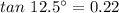
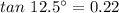
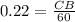
CB = 60 × 0.22
CB = 13.2 meters
Therefore the 13.2 meters from that point on the ocean floor to the wreck.