Answer:
The measure of angle CAD is 83 degrees.
Explanation:
Given information: ABCD is a parallelogram, AC is a diagonal,
 and
and
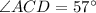 .
.
The opposite sides of parallelogram are congruent.
The diagonal AC divides the parallelogram in two congruent triangles.
In triangle ABC and ADC,
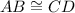 (Opposite sides of parallelogram)
(Opposite sides of parallelogram)
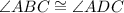 (Opposite angles of parallelogram)
(Opposite angles of parallelogram)
 (Opposite sides of parallelogram)
(Opposite sides of parallelogram)
By SAS postulate,
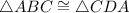
Since we know that opposite angles of parallelogram are equal, therefore
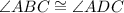

According to the angle sum property the sum of interior angles of a triangle is 180 degrees.
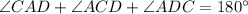
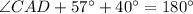
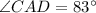
Therefore the measure of angle CAD is 83 degrees.