Explanation 1 P (3 or 4):
There are 40 number tiles numbered 1 to 40.
Multiple of 3 in 1 to 40 are:
There are 10 multiples till 30 (since
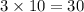 ) and then 33, 36, and 39 are other three multiples till 40. So there are 13 multiples of 3 from 1 to 40.
) and then 33, 36, and 39 are other three multiples till 40. So there are 13 multiples of 3 from 1 to 40.
Multiples of 4 in 1 to 40 are:
There are 10 multiples till 40 (since
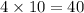 ) . So there are 10 multiples of 4 from 1 to 40.
) . So there are 10 multiples of 4 from 1 to 40.
Common Multiples of 3 and 4 in 1 to 40 is,
12, 28, 36, only 3
So, the probability of 3 or 4 is,

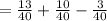
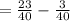
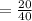
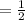
So the probability of 3 or 4 is
 .
.
Explanation 2 P(4 or 5):
Multiples of 4 in 1 to 40 are:
There are 10 multiples till 40 (since
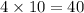 ) . So there are 10 multiples of 4 from 1 to 40.
) . So there are 10 multiples of 4 from 1 to 40.
Multiple of 5 in 1 to 40 are:
There are 8 multiples in 40 (since
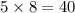 ). So there are 8 multiples of 5 from 1 to 40.
). So there are 8 multiples of 5 from 1 to 40.
Common Multiples of 4 and 5 in 1 to 40 is,
20 and 40 only 2
So, the probability of 4 or 5 is,
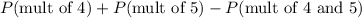
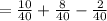
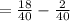
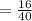
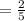
So the probability of 4 or 5 is
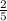 .
.