Question

Which equation describes the line which passes through the points (0. 17, 0) and (0, 0.51)

Answer 1

The equation of the line passing through the points (0, 17) and (0, 0.51) is x = 0.

Step-by-step explanation:

The equation of the line that passes through the points (0, 17) and (0, 0.51) can be found using the slope-intercept form of a linear equation, which is y = mx + b. To find the slope (m), we use the formula (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the two points.

1. Substituting the given points, we get m = (0.51 - 17) / (0 - 0) = -16.49 / 0, which is undefined.
2. Since the slope is undefined, we cannot write the equation in the slope-intercept form.
3. However, we can write the equation as x = 0, since the line passes through the x-coordinate of both points.

Answer 2

The equation of line which passes through the points (0. 17, 0) and (0, 0.51) is
`y=-3x+0.51`.

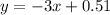Step-by-step explanation:

It is given that the line passing through the points (0. 17, 0) and (0, 0.51).

The slope of the line is

`m=(y_2-y_1)/(x_2-x_1)=(0.51-0)/(0-0.17)=-3`

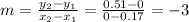
The slope intercept form of the line is

`y=mx+b`

Where, m is slope and b is y-intercept.

Equation of the line is

`y=-3x+0.51`

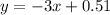
The other way to write the equation is shown below.

The point slope form of the line is

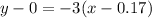`y-y_1=m(x-x_1)`

`y-0=-3(x-0.17)` ....(1)

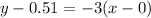`y-0.51=-3(x-0)` .....(2)

Therefore equation of line which passes through the points (0. 17, 0) and (0, 0.51) is
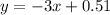`y=-3x+0.51`.