Question

In case 1, a block hanging on a spring oscillates with amplitude dd. in case 2, an identical block hanging on an identical spring oscillates with amplitude 2d2d. 1) compare the period of the oscillation in case 1 to the period of the oscillation in case 2.

Answer 1

period in case 2 is
`√(2)` times the period in case 1

Step-by-step explanation:

The period of oscillation of a spring is given by:

`T=2 \pi \sqrt{(m)/(k)}`

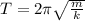
where

m is the mass hanging on the spring

k is the spring constant

Therefore, in order to compare the period of the two springs, we need to find their m/k ratio.

We know that when a mass hang on a spring, the weight of the mass corresponds to the elastic force that stretches the spring by a certain amplitude A:

`mg = kA`

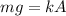
So we find

`(m)/(k)=(A)/(g)`

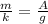
The problem tells us that the amplitude of case 1 is d, while the amplitude in case 2 is 2d. So we can write:

- for case 1:

`(m)/(k)=(d)/(g)`

`T_1=2\pi \sqrt{(d)/(g)}`

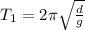
- for case 2:

`(m)/(k)=(2d)/(g)`

`T_2=2\pi \sqrt{(2d)/(g)}`

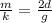
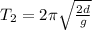
And by comparing the two periods, we find:

`(T_2)/(T_1)= √(2)`

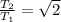
So, the period of oscillation in case 2 is
`√(2)` times the period of oscillation in case 1.