Question

What is the weight of a bowling ball with a 5 in. radius if we know that one cubic inch weighs 1/100th of a pound?

A. 6.54 lb.
B. 5.24 lb.
C. 9.86 lb.
D. 10.99 lb

Answer 1

The weight of a bowling ball is 5.24 pounds.

Option (B) is correct.

Explanation:

Formula

`Volume\ of\ a\ sphere = (4)/(3)\pi\ r^(3)`

Where r is the radius of a sphere.

As given

The radius of the ball is 5 in.

As the shape of the ball is spherical .

Thus

`Volume\ of\ a\ ball = (4)/(3)\pi\ 5^(3)`

`\pi = (22)/(7)`

Thus

`Volume\ of\ a\ ball = (4* 22* 5*\ 5* 5)/(3* 7)`

`Volume\ of\ a\ ball = (11000)/(21)`

Volume of a ball = 523.8 in³ (Approx)

As

`1\ in^(3) = (1)/(100)\ pound`

Thus

Convert 523.8 in³ into pounds.

`523.8\ in^(3) = (523.8)/(100)\ pound`

`523.8\ in^(3) = 5.24\ pound\ (Approx)`

Therefore the weight of a bowling ball is 5.24 pounds.

Therefore Option (B) is correct.

Answer 2

Option B is correct.

Weight of a bowling ball is 5.24 Ib

Explanation:

Assume: The shape of the bowling ball is perfectly spherical.

Given:

Radius of a bowling ball= 5 inches (r) .

One cubic inch weighs
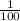`(1)/(100)`th of a pound.

Density of a bowling ball =
`(1)/(100) Ibs/in^3`

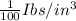
Volume of sphere is given by:

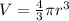`V = (4)/(3) \pi r^3` where V is the volume and r is the radius of the sphere.

Substitute the value of r =5 and
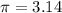`\pi = 3.14` in above we get;

`V = (4)/(3) \cdot 3.14 \cdot 5^3 =(4)/(3) \cdot 3.14 \cdot 125`

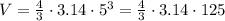
Simplify:

`V = 523.3333... in^3`

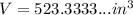
To find the weight of a bowling ball:

`Weight = Volume * Density`

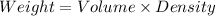
Then;

`Weight = 523.33333.. * (1)/(100) =(523.3333..)/(100) = 5.2333...`

Therefore, the weight of a bowling ball ≈ 5.24 Ib