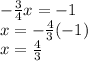Question

If 5/4x + 1/2 = 2x - 1/2 what is x

Answer 1

`x=(4)/(3)`

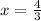
Explanation:

We can solve the equation by isolating x through order of operations. We use PEMDAS in reverse by undoing SADMEP or subtraction, addition, division, multiplication, exponents, and parenthesis.

`(5)/(4)x+(1)/(2) =2x-(1)/(2)`

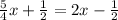
1. We simplify any parenthesis. Have none. So move on to the next step!

2. We undo any subtraction or addition by doing the inverse on both sides.

`(5)/(4)x+(1)/(2)-(1)/(2)  =2x-(1)/(2)-(1)/(2) \\(5)/(4)x =2x-1`

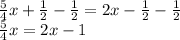
3. Now subtract an x term from both sides.

`(5)/(4)x-2x =2x-2x-1\\(5)/(4)x -(8)/(4)x =-1\\-(3)/(4)x=-1`

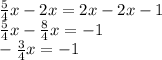
4. Divide both sides by the coefficient of x.

`-(3)/(4)x =-1\\x=-(4)/(3) (-1)\\x=(4)/(3)`