Question

Either Table A or Table B shows a proportional relationship.

Table A:

x −2 −1 0 1

y 2 3 0 5

Table B:

x −1 0 1 2

y −3 0 3 6

nvm you dont have to answer this i just found out the answer

Answer 1

Table B Shows proportional relationship.

Explanation:

Correct answers are the green and yellow dots. Hope this helps. The red dot I got wrong.

Answer 2

Table B shows a proportional relationship.

Explanation:

In a proportional relationship two quantities vary directly with each other. It means

`y\propto x`

`y=kx`

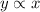
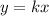
Where, k is the constant of variation.

The ordered pairs of table A are (-2,2), (-1,3), (0,0) and (1,5).

From these ordered pairs we can conclude that the value of y-coordinate is not changing according to the x-coordinate because the values of x increased by 1 for each ordered pair but the value of y is not increasing in the same proportion..

The ordered pairs of table B are (-1,-3), (0,0), (1,3) and (2,6). The value of y increasing at a constant rate 3 and the value of y-coordinate is 3 times of x-coordinate.

Choose any two ordered pairs of table B. Let the two points are (0,0) and (1,3), then the constant of variation is

`k=(y_2-y_1)/(x_2-x_1)=(3-0)/(1-0)=3`

The proportional relationship is defined as

`y=3x`

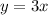
Therefore, 3 is the constant of variation and rate of change.

So, Table B shows a proportional relationship.