Answer:
D) 0.0796
Explanation:
Birth weights in Norway are normally distributed with a mean of 3570 g and a standard deviation of 500 g.
mean = 3570 and SD = 500
We need to find P(3500<x<3600)
P(3500<x<3600)= P(x=3600)- P(x=3500)
to find P(x=3600) we find z-score
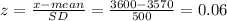
Now use z-score table . z-score = 0.5239
P(x=3600)=0.6179
to find P(x=3500) we find z-score
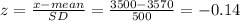
Now use z-score table . z-score = 0.4443
P(x=3600)=0.4443
P(3500<x<3600)= P(x=3600)- P(x=3500)
P(3500<x<3600)=0.5239-0.4443 = 0.0796