Question

Birth weights in Norway are normally distributed with a mean of 3570 g and a standard deviation of 500 g. Find the probability that 100 randomly selected birth weights have a mean between 3500 g and 3600 g.

A) 0.7257
B) 0.3551
C) 0.6449
D) 0.0796

Answer 1

Answer: 0.6449

(The one above is wrong)

Answer 2

D) 0.0796

Explanation:

Birth weights in Norway are normally distributed with a mean of 3570 g and a standard deviation of 500 g.

mean = 3570 and SD = 500

We need to find P(3500<x<3600)

P(3500<x<3600)= P(x=3600)- P(x=3500)

to find P(x=3600) we find z-score

`z= (x-mean)/(SD) =(3600-3570)/(500) =0.06`

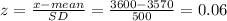
Now use z-score table . z-score = 0.5239

P(x=3600)=0.6179

to find P(x=3500) we find z-score

`z= (x-mean)/(SD) =(3500-3570)/(500) =-0.14`

Now use z-score table . z-score = 0.4443

P(x=3600)=0.4443

P(3500<x<3600)= P(x=3600)- P(x=3500)

P(3500<x<3600)=0.5239-0.4443 = 0.0796