Question

HELP!!!!!!!!!!!!!!!!!!!!!!

Answer 1

Explanation:

Please find the attachment.

We have been given an image on coordinate plane and we are asked to reflect our given image over the x-axis.

The rule for reflection for an image over x axis is:
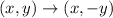`(x,y)\rightarrow(x,-y)`. This means that after reflection about x axis, x coordinates remain same but y-coordinates are transformed into their opposite sign.

Let us give names to vertices of our pre-image. A(-5,-1), B(-5,-4) and C(-2,-4).

When we will reflect our pre-image (ABC) about x-axis, x coordinates will remain same, so x coordinates will remain negative.

Since y-coordinates will change into their opposite sign, so coordinates of y will be positive for our image as y-coordinates of pre-image are negative.

A A'

(-5,-1) (-5,1)

B B'

(-5,-4) (-5,4)

C C'

(-2,-4) (-2,4)

Therefore, coordinates of our image A'B'C' will be: A'(-5,1), B'(-5,4) and C'(-2,4).

Answer 2

A) X = -5, Y = 1

B) X = -2, Y = 4

C) X = -5 , Y = 4

Explanation:

The reflection over an x-axis means the values associated with the x remains same while y-axis variable change their sign.

The three co-ordinates of this figure are

A) X = -5, Y = -1

B) X = -2, Y = -4

C) X = -5 , Y = -4

Now going by the above rule to determine the co-ordinates when the image is reflected over x-axis, the new co-ordinates are:

A) X = -5, Y = 1

B) X = -2, Y = 4

C) X = -5 , Y = 4