Answer:
- Equal midpoints of AC and BC.
- The product of the slopes of the diagonals AC and DB is -1.
Explanation:
1. Plot the given points, as you can see in the graph attached.
2. Calculate the midpoint of AC and DB:
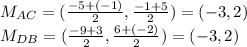
Therefore, the midpoint of AC and DB are equal.
3. Calculte the slope of the diagonals AC and DB:

4. Multiply the slopes of the diagonals:
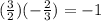 (AC and DB are perpendicular)
(AC and DB are perpendicular)