Question

Jonas is conducting an experiment using a 10-sided die. He determines that the theoretical probability of rolling a 3 is 1/10. He rolls the die 20 times. Four of those rolls result in a 3. Which adjustment can Jonas make to his experiment so the theoretical and experimental probabilities are likely to be closer?

A.) He can decrease the sample space.
B.) He can increase the sample space.
C.) He can decrease the number of trials.
D.) He can increase the number of trials.

Answer 1

Answer with explanation:

Number of faces of this unique Die = 10

Theoretical probability of rolling a 3
`=(1)/(10)`

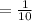
Now, the die is rolled 20, times.

Number of times, the rolls results in 3= 4

Probability of rolling '3'
`=(4)/(20)=(1)/(5)`

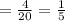
but, if you roll the die twenty times, Probability of rolling '3' should be
`=(2)/(20)=(1)/(10)`

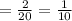
When we want, theoretical probability and experimental probability,match each other, the number of trials should be large enough to get closer and better results.

The adjustment can Jonas make to his experiment so the theoretical and experimental probabilities are likely to be closer:

D: He can increase the number of trials.

Answer 2

D. He can increase the number of trials.

Explanation:

Jonas is conducting an experiment using a 10-sided die. So the theoretical probability of rolling a 3 in a single trial is,
`(1)/(10)`

So the theoretical expected outcome of 3 in 20 roll would be,

`=(1)/(10)* 20=2`

But when he rolled the die 20 times, where four of those rolls resulted 3.

Which is 2 times more than the theoretical expectation.

Increasing the number of trials from 20, the expected outcome will increase.

As the number of trials is multiplied with
`(1)/(10)`, so bigger the number is from 20, bigger the value.

As we know,

`E(x)=n\cdot P(x)`

If we want to increase the expected value, we have to increase the number of trials.