Question

A sample of students from an introductory psychology class were polled regarding the number of hours they spent studying for the last exam. All students anonymously submitted the number of hours on a 3 by 5 card. There were 24 individuals in the one section of the course polled. The data was used to make inferences regarding the other students taking the course. There data are below:

4.5 22 7 14.5 9 9 3.5 8 11 7.5 18 20 7.5
9 10.5 15 19 2.5 5 9 8.5 14 20 8

Compute a 95 percent confidence interval. What does this tell us?

Answer 1

`8.68,13.16`

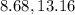
Explanation:

Hint- First we have to calculate the mean and standard deviation of the sample and then applying formula for confidence interval we can get the values.

Mean of the sample is,

`\mu=(\sum _(i=1)^(24)a_i)/(24)=(262)/(24)=10.92`

Standard deviation of the sample is,

`\sigma =\sqrt{(\sum _(i=1)^(24)\left(x_i-10.92\right)^2)/(24-1)}=5.6`

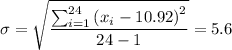
The confidence interval will be,

`=\mu \pm Z(\sigma)/(√(n))`

Here,

Z for 95% confidence interval is 1.96, and n is sample size which is 24.

Putting the values,

`=10.92 \pm 1.96\cdot (5.6)/(√(24))`

`=10.92 \pm 2.24`

`=8.68,13.16`

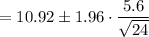
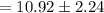
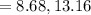
Confidence interval is used to express the degree of uncertainty associated with a sample.

95% confidence interval means that if we used the same sampling method to select different samples and calculate an interval, we would expect the true population parameter to fall within the interval for 95% of the time.