Question

The table shows the value of an account x years after the account was opened. Based on the exponential regression model, which is the best estimate of the value of the account 12 years after it was opened?

$8,910

$8,980

$13,660

$16,040

Answer 1

Option B is correct

$8,980

Explanation:

The equation of exponent regression is given by:

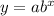`y=ab^x` , x is the time

where, a is the initial amount and b is the growth factor

As per the statement:

Let y represents the account value.

Given table as shown the value of an account x years after the account was opened.

Enter the values for x into one list and the values for y into the second list.

Now, graph the scatter plot as shown below in the attachment.

then, we get the equation of exponent regression:

`y = 4999.8 \cdot e^(0.0489x)`

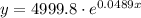
We can write this as:

`y = 4999.8 \cdot (e^(0.0489))^x`

⇒
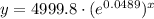
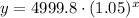`y = 4999.8 \cdot (1.05)^x` ...[1]

We have to find the best estimate of the value of the account 12 years after it was opened

Substitute x = 12 years in [1] we have;

`y = 499.8 \cdot (1.05)^(12)`

⇒
`y = 4999.8 \cdot 1.7959`

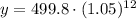
Simplify:

y ≈ $8979

Therefore, the best estimate of the value of the account 12 years after it was opened is, $8980

Answer 2

Correct choice is B

Explanation:

The equation of the exponential regression model is
`y=a\cdot b^x.`

1. When x=0,
`y=a\cdot b^0=a=5,000;`

2. When x=2, then

`y=5,000\cdot b^2=5,510\Rightarrow b^2=(5,510)/(5,000)=(551)/(500)=1.102,\ b=√(1.102)\approx 1.05.`

3. The equation of the function is
`y=5,000\cdot (1.05)^x.` Note that

• 
  `y(5)=5,000\cdot (1.05)^5\approx 6,381\approx 6,390;`
• 
  `y(8)=5,000\cdot (1.05)^8\approx 7,387\approx 7,390;`
• 
  `y(10)=5,000\cdot (1.05)^(10)\approx 8,144\approx 8,150.`

Therefore,

`y(12)=5,000\cdot (1.05)^(12)\approx 8,979\approx 8,980.`