Answer:
The length of CX is 22 ft.
Explanation:
Given information: In triangle ABC, F, G, and H are the midpoints of sides BC, CA, and AB respectively.
The medians FA, BG and CH intersect each other at point X.
According to the property of triangle, the intersection point of medians is called centroid and the centroid divides each median in 2:1.
Since X is centroid, therefore points X divides the median CH in 2:1, therefore we can say that CX:XH is 2:1.
It is given that the length of CX is 33.
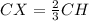
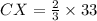
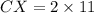
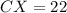
Therefore the length of CX is 22 ft.