Answer:
The jogging rate of Matthew is 5 mph.
Explanation:
Let the jogging rate of Matthew be x mph.
It is given that his jogging rate was 25 mph slower than the rate when he was riding. So, the riding rate is (x+25) mph.
The distance between Matthew and his friend's house is 12 miles.
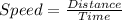
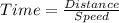
The time taken by Matthew in jogging is
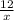 and the time taken by Matthew in riding is
and the time taken by Matthew in riding is
 .
.
It took him 2 hours longer to jog there than ride back.

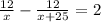
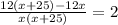
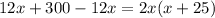
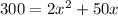
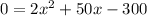
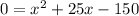
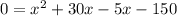
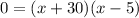
Equate each factor equal to 0.
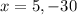
The speed cannot be negative, therefore the jogging rate of Matthew is 5 mph.