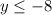Answer:
option C
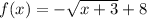
Explanation:
we have
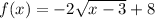
using a graphing tool
see the attached figure N

The range is the interval--------> (-∞,8]
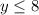
case A)
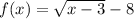
using a graphing tool
The range is the interval--------> [-8,∞)
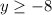
case B)
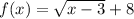
using a graphing tool
The range is the interval--------> [8,∞)
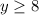
case C)
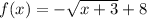
using a graphing tool
The range is the interval--------> (-∞,8]
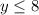
case D)
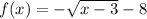
using a graphing tool
The range is the interval--------> (-∞,-8]