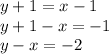1.
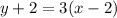
Point-slope form of the equation of a straight line is:
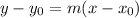 (1)
(1)
The two points in this case are:
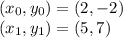
Slope of the line is given by:

Substituting into eq.(1), we find:
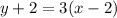
2.
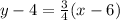
Point-slope form of the equation of a straight line is:
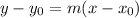 (1)
(1)
The two points in this case are:
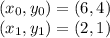
Slope of the line is given by:
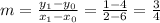
Substituting into eq.(1), we find:
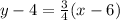
3.
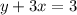
Standard form of the equation of a straight line is:
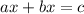
with a, b, c integer numbers.
Let's start by finding the point slope form first.
Point-slope form of the equation of a straight line is:
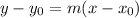 (1)
(1)
The two points in this case are:
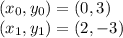
Slope of the line is given by:
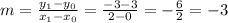
Substituting into eq.(1), we find:
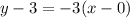
Now we can re-arrange the equation to re-write it in standard form:
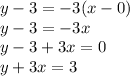
4.
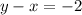
Standard form of the equation of a straight line is:
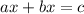
with a, b, c integer numbers.
Let's start by finding the point slope form first.
Point-slope form of the equation of a straight line is:
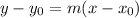 (1)
(1)
The two points in this case are:

Slope of the line is given by:
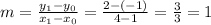
Substituting into eq.(1), we find:
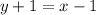
Now we can re-arrange the equation to re-write it in standard form: