Question

What is the value of cosθ given that (−2, 9) is a point on the terminal side of θ ? 985√85

−985√85

285√85

−285√85

Answer 1

-2√85 / 85

Explanation:

Answer 2

`cos\theta=(-2)/(√(85) )`

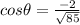
Explanation:

Let's call r the distance form the origin to the point (-2,9), this distance is related with
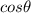`cos\theta` with the expression

`x=rcos\theta\\cos\theta=(x)/(r)`

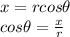
So, we have to find r with the formula of distance and the given point:

`r=\sqrt{x^(2)+y^(2)}=\sqrt{(-2)^(2)+(9)^(2) }\\r=√(4+81)=√(85)`

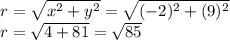
Now, replacing on the first relation, we have

`cos\theta=(-2)/(√(85) )`

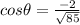
Therefore, the answer is

`cos\theta=(-2)/(√(85) )`

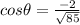
PD: choices were written wrong.