Answer:
C
Explanation:
This question should say "what are the roots or zeros of the function." The zeros or roots of a function are the x-intercepts. We find them by factoring and setting each factor equal to 0.
We can factor by grouping. We group two terms each into parenthesis and find the GCF of each pair. We should find a repeating factor of (x+2). We only keep one of these.
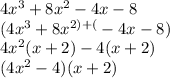
We set each factor equal to 0 and solve for x.
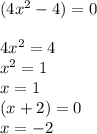
Our zeroes or roots are -2. -1. and 1. Answer C.