2 Answers

Sinan Guclu · Answer 1 · 2019-10-27T14:39:40+0000

Answer:

t = 2 s

Step-by-step explanation:

As we know that when object comes back to its initial position then the displacement of the object will be zero

so here we can say by kinematics equation

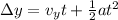
$\Delta y = v_y t + (1)/(2)at^2$

here we know that

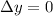
$\Delta y = 0$

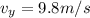
v_y = 9.8 m/s

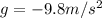
g = -9.8 m/s^2

now from above equation we know

$0 = 9.8 t - \frac{1]{2}9.8 t^2$

so from above equation we have

t = 2 s

Please log in or register to add a comment.