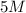Question

After reading 80\%80% of her e-mails in her inbox, Danette still has MM unread e-mails.

Which of the following expressions could represent the number of e-mails Danette had in her inbox before she started reading?
Choose 2 answers:
Choose 2 answers:

(Choice A)
A
\dfrac{M}{1-0.8}
1−0.8
M
​

(Choice B)
B
5M5M

(Choice C)
C
\dfrac{M}{0.8}
0.8
M
​

(Choice D)
D
1.8M1.8M

(Choice E)
E
80M80M

Answer 1

Answer: The correct options are.....

A)
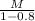`(M)/(1-0.8)` and

B)
`5M`

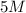
Explanation:

Suppose, the number of e-mails Danette had in her inbox before she started reading was
`X`.

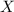Percentage of read emails is 80%, so the number of read emails
`= ((80)/(100)*X)=0.8X`

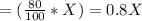
Thus, the number of unread emails
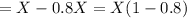`= X-0.8X=X(1-0.8)`, which is given as
`M`.

So, the equation will be........

`X(1-0.8)=M\\ \\ \Rightarrow X=(M)/(1-0.8) (Answer: 1) \\ \\ \Rightarrow X=(M)/(0.2)\\ \\ \Rightarrow X=((1)/(0.2))M=5M (Answer: 2)`

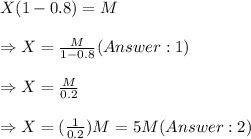
Thus, the expressions which could represent the number of e-mails Danette had in her inbox before she started reading are:
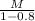`(M)/(1-0.8)` or
`5M`