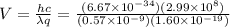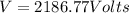We must use two formulas of energy first how energy is related to wavelength:
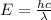
Such that
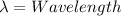 , c is the speed of light in a vacuum and h is Plank's constant.
, c is the speed of light in a vacuum and h is Plank's constant.
And the second equation is how energy relates to voltage:
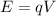
Such that q is the charge of the particle (in this case the electron) and V is voltage. By substituting the second equation into the first we have:
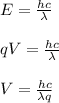
We know that:
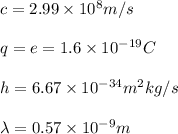
And so: