Question

How can you tell by looking at the coordinates of the two triangles that δ a'b'c' is a 180° rotation of δ abc?

a.the coordinates cannot prove a 180° rotation.

b.the y-coordinates of the points on δa'b'c' have opposite signs from the corresponding points on δabc.

c.the x-coordinates of the points on δa'b'c' have opposite signs from the corresponding points on δabc. eliminate

d.both the x and y coordinates of the points on δa'b'c' have opposite signs from the corresponding points on δabc?

Answer 1

Option d is correct.

Both the x and y coordinates of the point on δa'b'c' have opposite signs from the corresponding points on δabc.

Explanation:

The rule of 180 degree rotation about the origin is:

`(x, y) \rightarrow (-x , -y)`

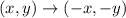
Since a Rotation of a point through 180°, about the origin when a point a(h, k) is rotated about the origin through 180° in anticlockwise or clockwise direction.

then, By the rule of 180 degree rotation;

`a(h, k) \rightarrow a'(-h , -k)`

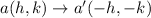
so, it takes the new position i.e,
`a'(-h , -k)`

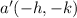
Therefore, both the x and y coordinates of the point on δa'b'c' have opposite signs from the corresponding points on δabc.