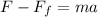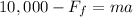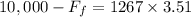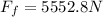Answer:
Part a)
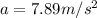
Part b)
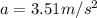
Part c)

Part d)
This difference in acceleration is due to some frictional force on the surface.
Part e)
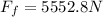
Step-by-step explanation:
Part a)
As we know by newton's II law
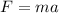
here we know that
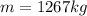

Now we have
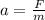
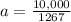
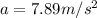
Part b)
distance covered by the car

t = 15 s
now by kinematics we have

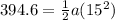
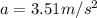
Part c)
Difference of acceleration is given as
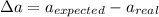
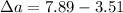

Part d)
This difference in acceleration is due to some frictional force on the surface.
Part e)
Now for magnitude of force is given as