Question

in parallelogram ABCD diagonals AC and BD intersect at Point E, BE = 2x^2 -3x + D = x^2 + 10 what is BD

Answer 1

Given the statement: In parallelogram ABCD, diagonals AC and BD intersects at point E.

Given that ABCD is a parallelogram.

As, we know that in a parallelogram diagonals bisect each other.

Since AC and BD intersect at E, and we get E is the mid point of both diagonals AC and BD.

⇒ BE = DE .....[1]

Substitute the given values of
`BE = 2x^2 -3x` and
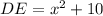`DE = x^2+10` in [1] we have;

`2x^2-3x = x^2+10`

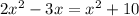
Subtract
`x^2` on both sides we get;

`2x^2-3x-x^2 = x^2+10-x^2`

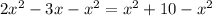
Simplify:

`x^2-3x =10`

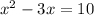
Subtract 10 on both sides we get;

`x^2-3x-10 =0`

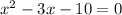
or

`x^2-5x+2x-10 =0`

`x(x-5)+2(x-5)=0`

`(x-5)(x+2)=0`

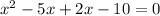
equate these factors equal to zero we get;

(x-5) = 0 and (x+2) = 0

we have;

x = 5 and x = -2

Since, x cannot be negative.

So, x =5

`BE = DE = x^2+10 = (5)^2+10 = 25+10 = 35 units`

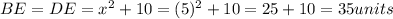
Diagonals BD = BE + DE = 35 + 35 =70 units.

Therefore, the value of BD = 70 units.