Question

Write an equation of a line (in standard form) that has the same slope as the line 3x-5y=7 and the same y-intercept as the line 2y-9x=8

Answer 1

5y - 3x = 20

Explanation:

we have to clear and from the equation and identify the equation of the form y = mx + b

3x - 5y = 7

3x - 7 = 5y

(3x - 7)/5 = y

3/5x - 7/5 = y

m = 3/5

we have to clear and from the equation and identify the equation of the form y = mx + b

2y - 9x = 8

2y = 9x + 8

y = (9x + 8)/2

y = 9/2 x + 4

b = 4

y = 3/5 x + 4

y - 3/5 x = 4

5y - 3x = 20

Answer 2

`3x-5y=-20`

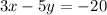
Explanation:

We can write the equation of a line in 3 different forms including slope intercept, point-slope, and standard depending on the information we have. We have two standard form equations which we will get a slope and a y-intercept from. We will convert each to slope intercept form to get the information. We will then write a new slope-intercept equation and convert to standard form.

3x-5y=7 has the same slope as the line. Let's convert.

`3x-5y=7\\3x-3x-5y=7-3x\\-5y=7-3x\\(-5y)/(-5)=(7-3x)/(-5) \\`

`y=(3)/(5)x -(7)/(5)`

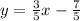
The slope is
`m=(3)/(5)`.

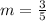2y-9x=8 has the same y-intercept as the line. Let's convert.

`2y-9x=8\\2y-9x+9x=8+9x\\2y=8+9x\\(2y)/(2)=(8+9x)/(2)`

`y=(8)/(2)+(9x)/(2)  \\y=4+(9)/(2)x`

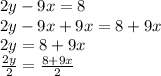
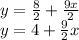
The y-intercept is 4.

We take
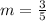`m=(3)/(5)` and b=4 and substitute into y=mx+b.

`y=(3)/(5)x+4`

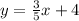
We now convert to standard form.

`-(3)/(5)x+y=(3)/(5)x-(3)/(5)x+4\\-(3)/(5)x+y=4`

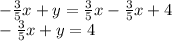
For standard form we need the coefficients of x and y to be not zero or fractions. We need integers but the coefficient of x cannot be negative. So we multiply the entire equation by -5 to clear the denominators.

`-5(-(3)/(5)x+y=4)\\3x-5y=-20`