Question

The population of a town increased by 15% in 2016, and decreased by 5% in 2017. If the population of the town was 60,000 in the beginning of 2016, then what was it at the end of 2017?

Answer 1

65,550.

Step-by-step explanation:

We have been given that the population of a town increased by 15% in 2016, and decreased by 5% in 2017.

Since an exponential is in form:
`a*b^x`.

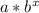For growth b=(1+r), where r in rate in decimal form.

For decrease b=(1-r), where r in rate in decimal form.

`15\text{ percent}=(15)/(100)=0.15`

Let us find the population increase in 2015.

`\text{Population at the end of year 2016}= 60,000*(1+0.15)^1`

`\text{Population at the end of year 2016}= 60,000*(1.15)`

`\text{Population at the end of year 2016}= 69,000`

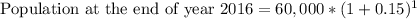
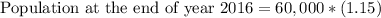
Therefore, the population at the end of year 2016 will be 69,000.

Now let us find population decrease of 5% in year 2017.

`15\text{ percent}=(5)/(100)=0.05`

`\text{Population at the end of year 2017}= 60,000*(1-0.05)^1`

`\text{Population at the end of year 2017}= 60,000*(0.95)`

`\text{Population at the end of year 2017}= 65,550`

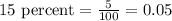
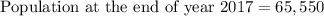
Therefore, the population at the end of year 2017 will be 65,550.