Answer:
0.234
Step-by-step explanation:
Given : You flip a fair coin 6 times
To Find: What is the probability that you will get exactly 4 tails
Solution:
Formula :
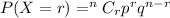
Where r is the no. of success
n is the total no. of trials
p is the probability of success
q is the probability of failure
In This case success is getting tail
So, Probability of getting tail =

So, Probability of not getting tail =

n = 6
r = 4
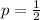
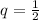
Substitute the values in the formula
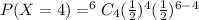
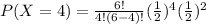
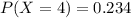
Hence the probability that you will get exactly 4 tails is 0.234