Answer:
Arithmetic and divergent sequence.
Explanation:
We have been given a sequence:
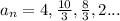
Arithmetic sequence: It is the sequence in which the difference (known as common difference) between consecutive terms is same
Formula for difference:
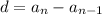
Geometric sequence: It is the sequence in which the ratio (known as common ration) between consecutive terms is same.
Formula for ratio:
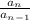
Here, we will first check the common difference

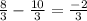

Hence, we are getting common difference therefore it is an arithmetic sequence.
Arithmetic sequence always diverges
And given sequence being arithmetic will diverge.