Question

A ball is dropped from a heigh of h feet and repeatedly bounces off the floor. After each bounce, the ball reaches a height that is 2/3 of the height feom which it oreviously fell. For example, after the first bounce, the ball reaches a height of 2/3h feet. What represents the total number of feet the ball travels between the firat and the sixth bounce?

Answer 1

`s = \sum^5_1 {(2h)((2)/(3))^i},`

Explanation:

The initial height of the ball is h

After the first bounce the height is
`(2)/(3)h`

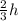
After the second bounce the height is
`(2)/(3)((2)/(3))h`

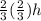
After the i-th rebound the height is
`((2)/(3)) ^ i`

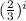
Then, distance s traveled by the ball is the sum of the heights reached between the first and fifth bounces.

`s = 2 [(2)/(3)h + (2)/(3)((2)/(3))h +, ..., + ((2)/(3)) ^ n h]`

The equation is multiplied by 2 because the distance the ball travels when it goes up is the same as it travels down.

Finally the distance is a geometric series as shown:

`s = \sum^5_1 {(2h)((2)/(3))^i},`