Answer:
We can compare slopes and y-intercepts. The first equation has m=3/4 and b=7. The second has m=-2/5 and b=2. They are intersecting lines.
Explanation:
These equations are in the standard form of a line. We can convert to the slope-intercept by solving for y.
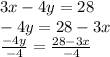
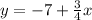
We can now convert the second equation.
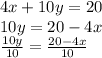
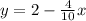
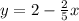
We can compare slopes and y-intercepts. The first equation has m=3/4 and b=7. The second has m=-2/5 and b=2. They are intersecting lines. This eliminates A and B. The answer based on the information given is likely D.