Question

An airplane must clear a 60-foot pole at the end of a runway 500 yards long determine the angle of elevation at which the airplane must ascend to clear the pole.

Answer 1

2.3 degrees.

Explanation:

Please find the attachment.

We are told that an airplane must clear a 60-foot pole at the end of a runway 500 yards long.

Let us convert 500 yards to feet.

1 yard= 3 feet.

500 yards= 3*500 feet= 1500 feet.

We can see from our attachment pole and runway are in form of a right triangle. The pole is opposite to angle of elevation of plane and length of runway is adjacent.

Since tangent represents the relation between opposite and adjacent of right triangle, So we will use tangent to find angle of elevation that plane must ascend to clear the pole.

`tan(\theta)=(60)/(1500)`

`\theta=\tan^(-1)((60)/(1500) )`

`\theta=\tan^(-1)(0.04)`

`\theta=2.290610042639`

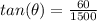
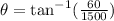
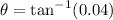
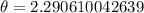
Therefore, the airplane must ascend 2.3 degrees to clear the pole.