Question

Hey conic section has the equation X+Y^2+ 12X + 8y= 48 determine the following type of conic domain and range axis of symmetry and center?

Answer 1

Axis of symmetry are lines x=-6 and y=-4, center (-6,-4)

Explanation:

Consideer the equation
`x^2+y^2+12x+8y=48.`

First, complete perfect squares:

`(x^2+12x)+(y^2+8y)=48,\\ \\(x^2+12x+36-36)+(y^2+8y+16-16)=48,\\ \\(x+6)^2+(y+4)^2-36-16=48,\\ \\(x+6)^2+(y+4)^2=100.`

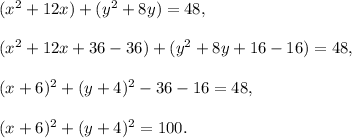
This equation represents a circle with center at point (-6,-4) and radius r=10.

Axis of symmetry are lines x=-6 and y=-4 (vertical and horizontal lines passing through the center).