Answer:
option A
Explanation:
The following ordered pairs are solutions to a linear equation: (-20, 11.5), (-21, 12), and (-22, 12.5).
Frame the equation of line y=mx+b using ordered pairs
(-20, 11.5), (-21, 12)
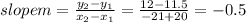
m= -0.5
Now plug in (-21,12) and find out b
y=mx+b
12= -0.5(-21) + b
12= 10.5 +b
Subtract 10.5 on both sides
So b= 1.5
Equation of line is y=-0.5x + 1.5
Slope is negative so graph will be decreasing
Option A and option C graphs are decreasing
y intercept is the b values = 1.5
y intercept is (0,1.5)
Lets find x intercept
Plug in 0 for y in the equation y=-0.5x+1.5
0 = -0.5x+1.5
subtract 1.5 on both sides
1.5 = -0.5x
Divide by -0.5
so x= 3
So x intercept is (3,0)
Option A graph has x intercept (3,0) and y intercept (0,1.5)