Question

write an equation in slope intercept form of a line that passes through the point (14, 8) and is (a) parallel (v) perpendicular to the line that passes through the points (4,9) and (-3, 6)

Answer 1

`y-8=-(7)/(3) (x-14)`

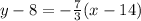
Explanation:

We can write the equation of a line in 3 different forms including slope intercept, point-slope, and standard depending on the information we have. We have a point and a slope from the equation. We will chose point-slope since we have a point and can find the slope.

Point slope:
`y-y_1=m(x-x_1)`

We must find the slope using the slope formula.

Slope:
`m=(y_2-y_1)/(x_2-x_1)`

We substitute
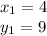`x_1=4\\y_1=9` and
`x_2=-3\\y_2=6`

`m=(6-9)/(-3-4)`

`m=(6-9)/(-3-4)=(-3)/(-7) =(3)/(7)`

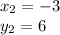
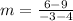
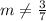`m\\eq (3)/(7)` in our new equation because it is perpendicular to it. This means we will need to change it into its negative reciprocal which is
`m=-(7)/(3)`.

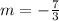We will substitute
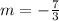`m=-(7)/(3)` and
`x_1=14\\y_1=8`.

`y-8=-(7)/(3) (x-14)`

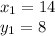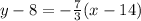
This is the equation of the line perpendicular to the equation line through the points given that crosses through (14,8).